Measuring the Elastic Modulus of Thin Film Annuli Using capillary wrinkling
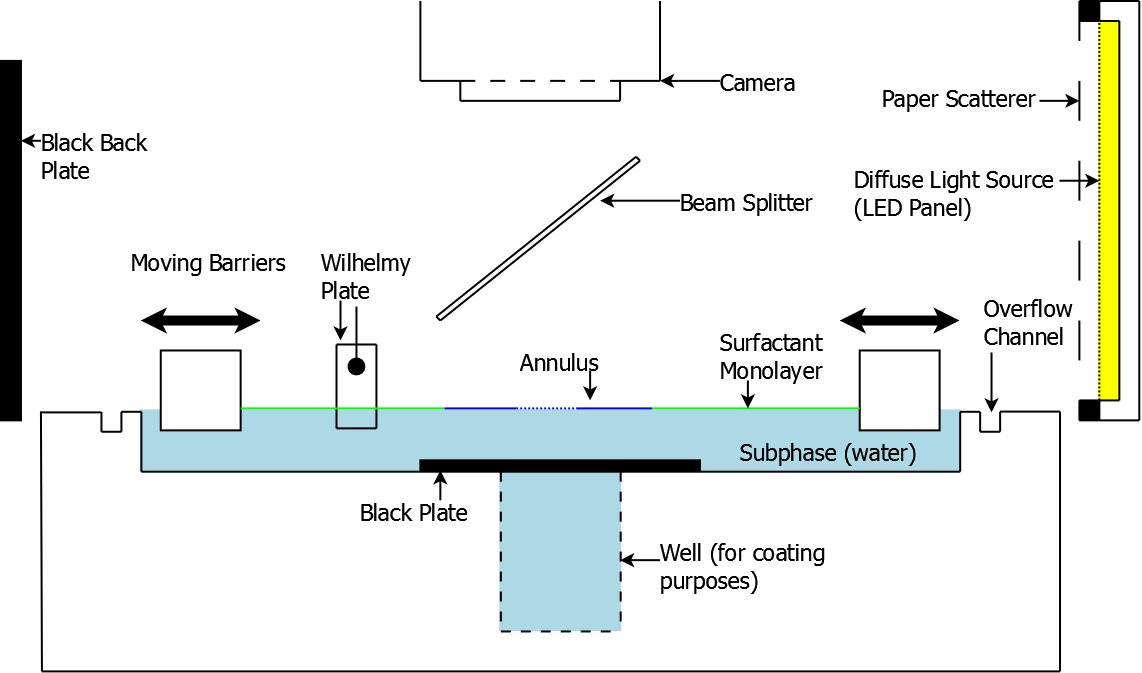
For my 3rd year project/BSc dissertation equivalent, my lab partner Dom and I were paired up and set to work on improving some work done as a side project of Dr. David Farmer's PhD thesis. His project consisted of cutting annuli into ultra-thin films of polystyrene (<200nm) and floating them on water. The surface tensions on the inside and outside of the annuli were equal and opposite, generated by the capillary interactions at the inner and outer edges. A Langmuir-Blodgett trough, which is a device used to control the surface density of an immiscible addition to the subphase. In our case we added span 80, a surfactant, to the water outside of the annuli. The density of the surfactant could be adjusted using the trough, and the surface tension was simultaneously measured. The increasing density of the surfactant acted to reduce the surface tension down from the value of water to the value of span 80 by replacing the surface water with span 80.
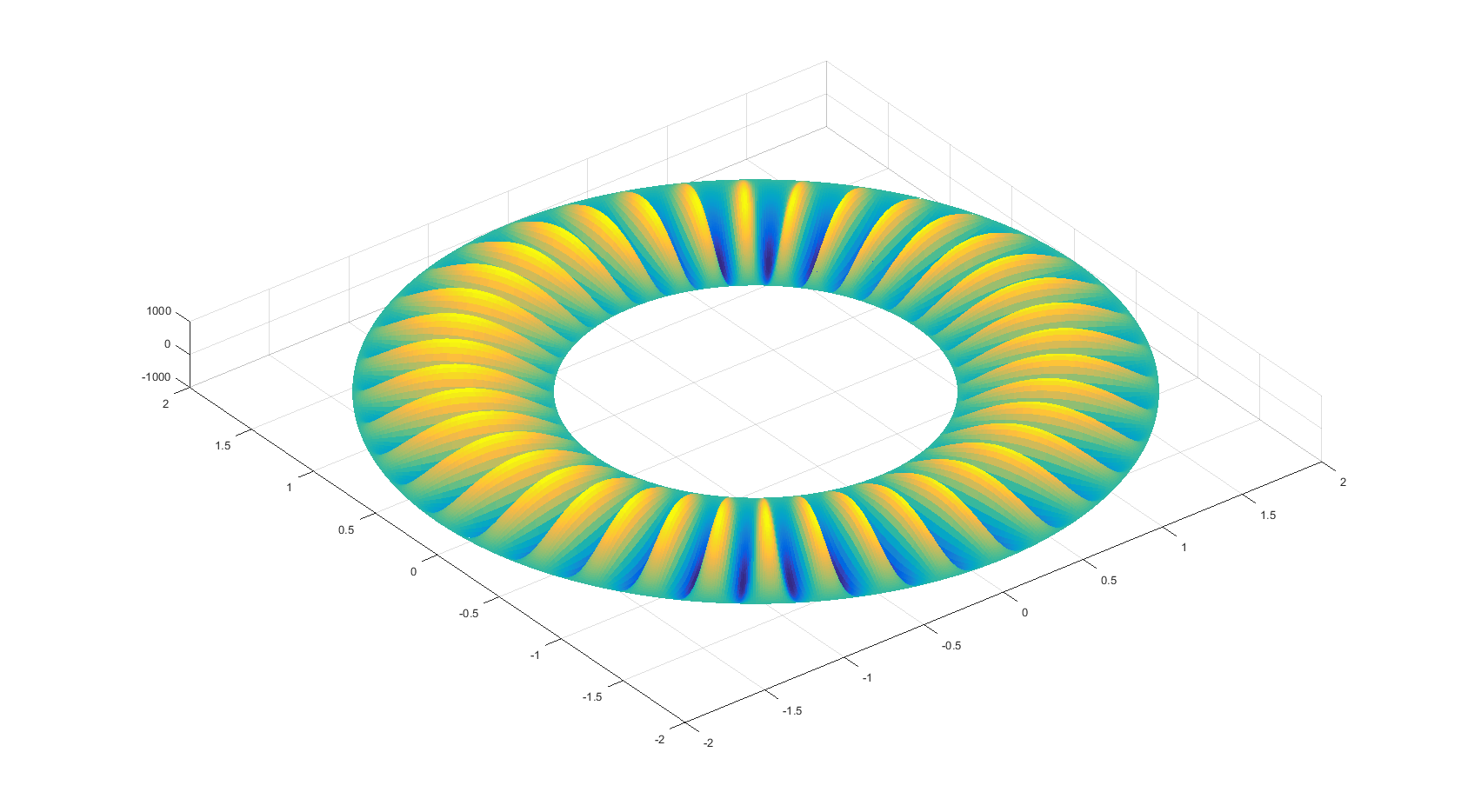
This lead to an imbalance of forces acting on the inner circumference and the outer circumference. When the difference in force was strong enough, the annulus would wrinkle according to an expression that was to be determined. The energy of the wrinkled and unwrinkled states would be equal at a certain force, referred to as the nucleation pressure, and a sinusoidal distribution film position was predicted. Unfortunately, defects in the films and surface tension lead to collapsing of wrinkles and disturbed the sinusoidal distribution. Instead, the wrinkles formed with stochastic position and varying amplitudes, leading to the aforementioned collapsing flaps.
The aim of the experiment was to count the wrinkles that formed using a high resolution grey scale camera and some image processing scripts in MATLAB to determine the number of wrinkles as a function of the difference in surface tension and to use this, alongside a theoretical prediction of the number of wrinkles, to extract the elastic modulus. The resulting equations, which were not derived ab initio and instead built upon David's empirical approach, were unwieldy and inaccurate. They always contained an offset, which we put down to defects and contaminants in the water such as dust and residual surfactants.
After the project was completed and I'd had a break, I attempted to derive the form of the wrinkling from first principles using the 3D stress and strain relations and the known initial conditions and constraints. The resulting differential equations were intractable and required a lot of work and yielded similarly as horrendous equations as before. Because the equations are so unwieldy, the technique was decided to be infeasible and impractical, leaving it abandoned.